Remove ads

We have detected that Javascript is not enabled in your browser. The dynamic nature of our site means that Javascript must be enabled to function properly. Please read our terms and conditions for more information.

Note by Landon Valencia , created more than 1 year ago

Notes on the various theorems that are tested on the Geometry Regents.

339

	Created by Landon Valencia almost 11 years ago

Rate this resource by clicking on the stars below:

(2)

Ratings (2)

2
0
0
0
0

0 comments

There are no comments, be the first and leave one below:

To join the discussion, please sign up for a new account or log in with your existing account.

Geometry Regents - Theorem Review Notes

1/1

Theorem #1: If 2 angles form a linear pair, then they are supplementary.

Unit 1

Theorem #2: If 2 angles are complementary to the same angle, they their measures are equal.

Theorem #3: If 2 angles are supplementary to the same angle, then their measures are equal.

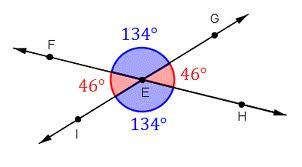
Two angles are congruent if they have the equal measures.

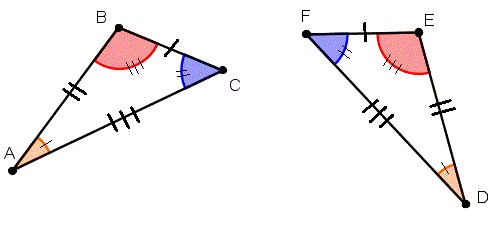
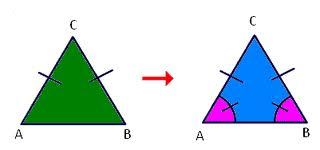
Theorem #4: If 2 angles are vertical angles, then they are congruent.

Two triangles are congruent if their corresponding parts are congruent.

SSS Postulate: If 3 pairs of corresponding sides of 2 triangles are congruent then the two triangles are congruent.

ASA postulate: If 2 pairs of corresponding angles in the 2 triangles and the side in between them are congruent, then the 2 triangles are congruent.

SAS postulate: If 2 pairs of corresponding sides in the 2 triangles and the angle in between them are congruent, then the 2 triangles are congruent.

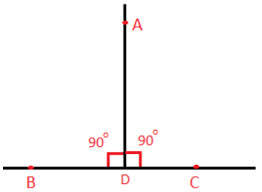
Theorem #5: All right angles are congruent

Theorem #6: Addition theorem of congruence

Theorem #7: Subtraction theorem of congruence

If 2 angles are congruent, then their corresponding parts are congruent.

AAS postulate: If two angles and the non-included side of one triangle are congruent the other, then the 2 triangles are congruent.

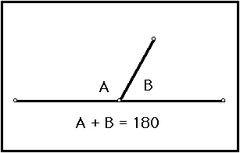
Theorem #8: If 2 supplementary angles are congruent, then they are right angles.

Hypotenuse-Leg Postulate: If the hypotenuse and a pair of legs in 2 right triangles are congruent, then the 2 triangles are congruent.

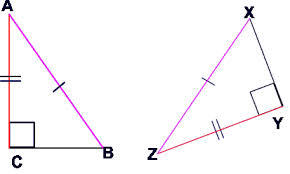
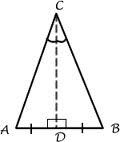
Theorem #9: (Base-Angle Theorem) If a triangle has 2 congruent sides, the 2 angles opposite those sides are congruent.

Isosceles Triangle Property (Little Theorem): If a triangle is isosceles, then its' median, angle bisector, and altitude coincide.

Theorem #10: A triangle is isosceles if its median, angle bisector, and altitude from the vertex angle coincide.

Unit 1