In this our final study note on our series on Differentiation and Integration, we look at definite integrals. Using graphs we demonstrate the key points that you need to understand to master the topic. Sample equation questions are then provided to allow you to check your learning progress.
Pinned to
87
0
0
No tags specified

|
Created by Niamh Ryan
almost 8 years ago
|
|
Rate this resource by clicking on the stars below:




 (0)
(0)
Ratings (0)
| 0 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 |
0 comments
There are no comments, be the first and leave one below:
Close
9834721
note
2018-10-05T12:05:12Z
4/4
Example 3
Example:
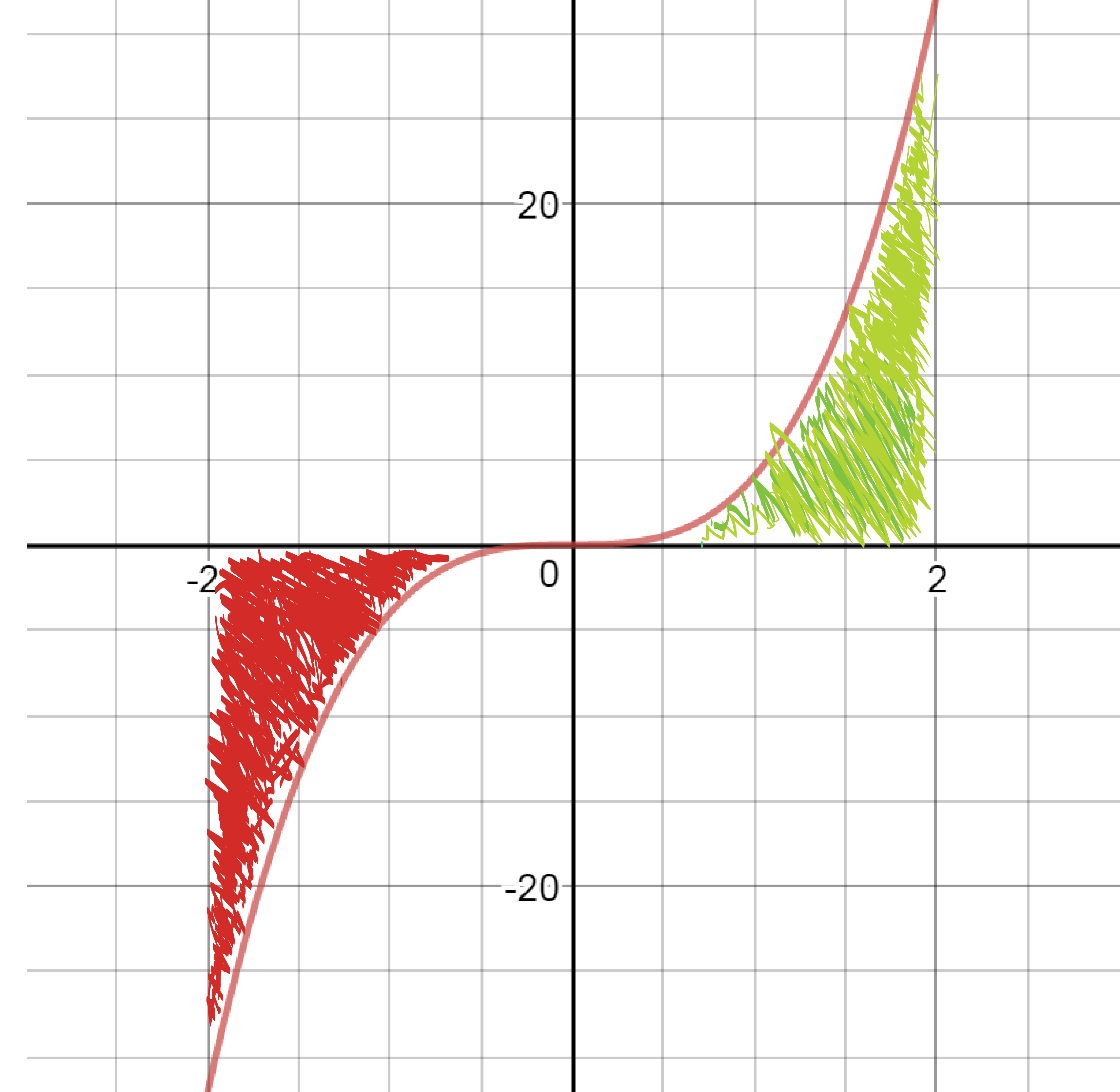
Find the area enclosed by the function f(x)=4x3 between x=−2 and x=2\\
Answer:
If we integrate this as usual, we will get answer that doesn't make sense. ∫2−24x3dx=[x4]2−2=24−(−2)4=0
Clearly , as you can see in the graph below, the area enclosed by the function isn't zero. The integration has given us an answer of zero because it counts area below the x-axis as negative area. To find the absolute value of the area, we must calculate the area enclosed by the function from x=−2 to x=0 and x=0 to x=−2 separately.
∫204x3dx=[x4]20=24−(0)4=16
∫0−24x3dx=[x4]0−2=0−(−2)4=−16
Now, to find the area, we sum the absolute value of these two integrands. Area=16+∣−16∣=32