Mathematik Note on Themen der Vektorrechnung II, created by Paula Raithel on 11/10/2016.
|
|
Created by Paula Raithel
almost 9 years ago
|
|




 (2)
(2)
| 2 | ||
| 0 | ||
| 0 | ||
| 0 | ||
| 0 |
0 comments
There are no comments, be the first and leave one below:
Von den Koordinatensystemen her wisst ihr inzwischen hoffentlich, was ein Punkt ist: In der Ebene zum Beispiel P(3;4) oder im Raum zum Beispiel P(2;1;3). Und Vektoren kennt ihr in Zwischenzeit ebenfalls, sowohl in der Ebene als auch im Raum. Zur Erinnerung: Der Vektor gibt euch eine Richtung an. Dieses Wissen kombinieren wir im nun Folgenden.
Beispiel:
Gegeben sei eine Gerade durch einen bestimmten Punkt mit einem Richtungsvektor. Die Punktrichtungsgleichung soll aufgestellt werden. Seht euch dazu einmal die folgende Berechnung an. Einige Erklärungen dazu folgen im Anschluss.
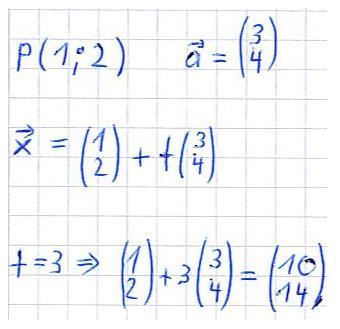
Wie bereits oberhalb der Rechnung beschrieben, haben wir einen Punkt und einen Vektor, mit welchem wir die Punktrichtungsgleichung bestimmen. Setzen wir nun für t eine Zahl ein ( z.B. t = 3 in unserem Beispiel ) erhalten wir einen weiteren Punkt P(10;14), welcher ebenfalls auf der Geraden liegt.
Die Aufgabe könnte auch umgekehrt laufen. Ihr kennt die Punkte P1(10;14) und P2(1;2) und die Richtung und sollt nun "t" berechnen. Dies würde dann wie folgt aussehen: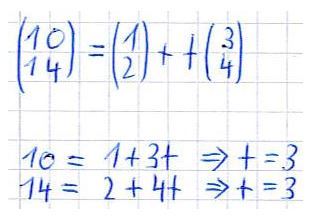
Man erhält ein lineares Gleichungssystem, welches mit t=3 für alle Gleichungen gelöst werden kann.
Punktrichtungsgleichung im Raum
Die eben durchgeführten Rechnungen funktionieren natürlich auch im Raum. Es steht dann in den jeweiligen Fällen noch ein z-Wert und das Gleichungssysteme hat drei Zeilen.