Mathematik Note on Themen der Vektorrechnung II, created by Paula Raithel on 11/10/2016.
Pinned to
317
18
0
No tags specified
|
|
Created by Paula Raithel
almost 9 years ago
|
|
Close
6633925
note
2017-01-14T00:32:19Z
4/6
Abstand paralleler Geraden
Lage von Geraden zueinander
Lage von Geraden zueinander
Zwei Geraden können verschiedene Lagen zueinander einnehmen:
- Zwei Geraden liegen aufeinander
- Beide Geraden sind zueinander parallel
- Die beiden Geraden schneiden sich in einem Punkt
- Die beiden Geraden sind windschief ( verlaufen weder parallel noch schneiden sich )
In diesem Artikel interessieren wir uns für den Fall Nummer 2: Die Geraden sind zueinander parallel. Dies sieht dann wie folgt aus:
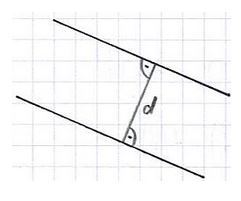
Fragt sich jetzt noch: Wie sehe ich in der mathematischen Darstellung, ob die Geraden parallel zueinander sind? Antwort: Dies sieht man an der linearen Abhängigkeit der beiden Richtungsvektoren. Die beiden Richtungsvektoren sind kollinear.
Beispiel:
Wir sehen uns im nun Folgenden zwei Geraden an. Diese sind parallel, denn die beiden Vektoren sind vielfache voneinander: Multipliziert man den ersten Vektor mit drei, erhält man den zweiten Vektor.
Abstand zweier paralleler Geraden
Nun möchten wir den Abstand zwischen zwei parallelen Geraden
berechnen. Dazu erst einmal die allgemeine Formel, gefolgt von einem
wahrscheinlich deutlich besser verständlichem Beispiel:
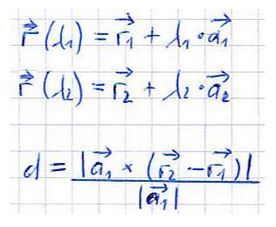
Beispiel:
Im nun Folgenden soll der Abstand zwischen zwei Geraden berechnet werden. Um die Rechnung zu verstehen, müsst ihr das Kreuzprodukt und die Betragsbildung verstehen.